Qu'est-ce que le binaire? [La technologie expliquée]

Publicité

Étant donné que le binaire est si fondamental pour l'existence des ordinateurs, il semble étrange que nous n'ayons jamais abordé le sujet avant - donc aujourd'hui, je pensais que je donnerais un bref aperçu de ce que le binaire signifie réellement et comment il est utilisé dans des ordinateurs. Si vous vous êtes toujours demandé quelle est la différence entre 8 bits, 32 bits, et 64 bits est vraiment, et pourquoi c'est important - alors lisez la suite!

Qu'est-ce que le binaire? La différence entre Base 10 et Base 2

La plupart d'entre nous ont grandi dans un monde de base de 10 chiffres, ce qui veut dire que nous avons 10 'base' Nombres (0-9) dont nous dérivons tous les autres nombres. Une fois que nous les avons épuisés, nous montons d'un niveau d'unité - 10, 100, 1000 - cette forme de comptage est martelée dans nos cerveaux dès la naissance. En fait, ce n'est qu'à partir de la période romaine que nous avons commencé à compter en base 10. Avant cela, la base 12 était la plus facile et les gens utilisaient leurs phalanges pour compter.

Lorsque nous apprenons la base 10 à l'école primaire, nous écrivons souvent les unités comme ceci:

Donc, le nombre 1990 se compose en fait de 1 x 1000, 9 x 100, 9 x 10, et 0 x 1. Je suis sûr que je n'ai pas besoin d'expliquer la base 10 plus loin que cela.

Mais si au lieu d'avoir une sélection complète de 0,1,2,3,4,5,6,7,8,9 de travailler avec comme numéros de base - et si nous avions seulement 0, et 1. C'est appelé base 2; et il est aussi communément appelé binaire. Dans un monde binaire, vous ne pouvez que compter 0,1 - alors vous devez passer au niveau d'unité suivant.

Compter en binaire

Cela aide énormément si nous écrivons les unités lors de l'apprentissage du binaire. Dans ce cas, au lieu que chaque unité supplémentaire soit multipliée par 10, elle est multipliée par 2, ce qui nous donne 1,2,4,8,16,32,64 … Donc, pour aider à calculer, nous pouvons les écrire comme ceci:

En d'autres termes, la valeur la plus à droite dans un nombre binaire représente le nombre de 1. Le chiffre suivant, à gauche de celui-ci, représente le nombre de 2. Le suivant représente le nombre de 4… et ainsi de suite.

Avec cette connaissance, nous pouvons écrire un tableau de comptage en binaire, avec la valeur de base 10 équivalente indiquée à gauche.

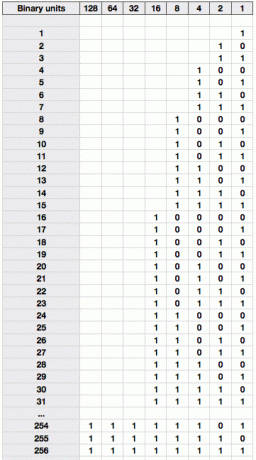
Passez un moment à le parcourir jusqu'à ce que vous compreniez exactement pourquoi 25 est écrit 11001. Vous devriez pouvoir le décomposer comme étant 16 + 8 + 1 = 25.

Travail en arrière - base 10 en binaire

Vous devriez maintenant être en mesure de déterminer la valeur d'un nombre binaire en dessinant un tableau similaire et en multipliant chaque unité. Changer un nombre de base 10 normal en binaire demande un peu plus d'effort. La première étape consiste à trouver la plus grande unité binaire qui «s'inscrit» dans le nombre. Ainsi, par exemple, si nous faisions 35, alors le plus grand nombre de ce tableau qui correspond à 35 est 32, donc nous aurions un 1 là dans cette colonne. Nous avons alors un reste de 3 - qui aurait besoin d'un 2, puis enfin d'un 1. Nous obtenons donc 100011.

8 bits, octets et octets

Le tableau que j'ai montré ci-dessus est de 8 bits, car nous avons un maximum de 8 zéros et uns à utiliser pour notre nombre binaire. Ainsi, le nombre maximum que nous pouvons éventuellement représenter est 11111111, ou 255. C’est pourquoi, pour représenter un nombre quelconque de 0-255, nous avons besoin d'au moins 8 bits. Octet et Byte est simplement une autre façon de dire 8 bits. Donc 1 octet = 8 bits.

Informatique 32 vs 64 bits

De nos jours, vous entendez souvent les termes Versions 32 bits et 64 bits de Windows, et vous savez peut-être que Windows 32 bits ne peut prendre en charge jusqu'à 4 gigaoctets de RAM. Mais pourquoi?

Tout se résume à l'adressage de la mémoire. Chaque bit de mémoire a besoin d'une adresse unique pour y accéder. Si nous avions un 8 bits système d'adressage mémoire, nous ne pourrions avoir qu'un maximum de 256 octets de la mémoire. Avec un 32 bits système d'adressage mémoire (imaginez étendre le tableau ci-dessus pour avoir 32 colonnes d'unité binaire), nous pouvons aller partout 4,294,967,296? 4 milliards d'octets, ou en d'autres termes - 4 GIGAoctets.64 bits l'informatique supprime essentiellement cette limite en nous abandonnant à 18 quintillions différentes adresses - un certain nombre d'entre nous ne savent tout simplement pas.

Adressage IPv4

Le dernier souci du monde informatique est tout sur les adresses IP IPv6 et ARPAgeddon à venir [Explication de la technologie] Lire la suite , en particulier IPv4 adresses, comme celles-ci:

• 192.168.0.1
• 200.187.54.22

Ils se composent en fait de 4 nombres, chacun représentant une valeur jusqu'à 255. Pouvez-vous deviner pourquoi? Oui, l'adresse entière est représentée par 4 octets (32 bits au total). Cela ressemblait à énormément d'adresses possibles (environ 4 milliards en fait) au moment où Internet a été inventé pour la première fois, mais nous commençons rapidement à manquer maintenant que tout dans notre vie doit être connecté. Pour résoudre ce problème, le nouveau IPv6 utilise 128 bits au total, ce qui nous donne environ 340 milliards de dollars (mettre 38 zéros à la fin) des adresses avec lesquelles jouer.

Je vais le laisser là pour aujourd'hui, donc je peux revenir à mon objectif initial qui était d'écrire le prochain tutoriel Arduino - dans lequel nous utilisons largement un registre à décalage de bits. J'espère qu'aujourd'hui vous a donné une compréhension de base de la façon dont le binaire est si important pour les ordinateurs, pourquoi les mêmes nombres continuent à apparaître et pourquoi le nombre de les bits que nous devons représenter quelque chose placent une limite finie sur la quantité de mémoire, la taille de l'écran, les valeurs de couleur possibles ou les adresses IP uniques à notre disposition. La prochaine fois, nous verrons calculs de logique binaire, ce qui est à peu près tout ce qu'un processeur d'ordinateur fait, ainsi que la façon dont les ordinateurs peuvent représenter des nombres négatifs.

Commentaires? Confusion? Avez-vous trouvé mon explication facile à comprendre? Dans tous les cas, merci de nous contacter dans les commentaires. Je vous laisse avec une blague binaire!

Il n'y a que 10 types de personnes dans le monde: ceux qui comprennent binaireet ceux qui ne le font pas.

Crédit d'image: Shutterstock