Si vous avez suivi un cours sur les structures de données dans le cadre de votre diplôme en informatique ou si vous êtes un programmeur autodidacte, il est probable que vous ayez rencontré le terme « arbres binaires ». Bien qu'ils puissent sembler un peu écrasants et complexes, le concept d'un arbre binaire est assez simple.
Continuez à lire pendant que nous disséquons les arbres binaires et pourquoi ils sont un concept de base nécessaire pour les programmeurs.
Que sont les arbres binaires ?
Les arbres binaires font partie des premières structures de données enseignées aux étudiants dans un cours sur les structures de données. Un arbre binaire est composé de nombreux nœuds, et chaque nœud de l'arbre binaire contient deux pointeurs qui indiquent les nœuds de données enfants gauche et droit.
Le premier nœud d'un arbre binaire est appelé la « racine ». Les nœuds du dernier niveau d'un arbre sont appelés feuilles.
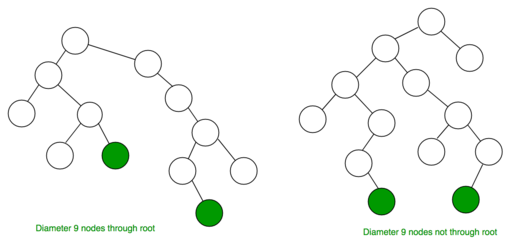
Chaque nœud contient un élément de données et deux pointeurs de nœud. Un arbre binaire vide est représenté par un pointeur nul. Comme vous l'avez peut-être déjà compris, les arbres binaires ne peuvent avoir que deux enfants (d'où le nom).
Types d'arborescences binaires
Il existe plusieurs arborescences binaires différentes selon la façon dont les nœuds sont positionnés. Un arbre binaire est appelé arbre binaire complet lorsque chaque nœud de l'arbre a zéro ou deux enfants. Dans un arbre binaire parfait, tous les nœuds ont deux enfants et les feuilles sont toutes à la même profondeur.
En rapport: Meilleures façons d'apprendre à coder gratuitement
Un arbre binaire complet a des nœuds remplis à chaque niveau, à l'exception du dernier niveau. Dans les arbres binaires complets, les nœuds sont concentrés sur le côté gauche de la racine. Une autre structure courante est un arbre binaire équilibré; dans cette structure, les hauteurs des sous-arbres droit et gauche doivent différer d'au plus un. Il est également nécessaire que les sous-arbres gauche et droit soient également équilibrés.
Il est important de noter que la hauteur de l'arbre binaire équilibré est O(logn), où n est le nombre de nœuds dans l'arbre.
Dans certains cas, si chaque nœud n'a qu'un seul enfant gauche ou droit, alors l'arbre binaire peut devenir un arbre binaire asymétrique. Il se comportera alors comme une liste chaînée, de tels arbres sont aussi appelés arbre dégénéré.
Que sont les arbres de recherche binaire ?
Un arbre binaire de recherche (BST) est essentiellement un arbre binaire ordonné avec une propriété spéciale connue sous le nom de propriété « arbre de recherche binaire ». La propriété BST signifie que les nœuds avec une valeur de clé inférieure à la racine sont placés dans le sous-arbre de gauche, et les nœuds avec une valeur de clé supérieure à la racine font partie du sous-arbre de droite.
La propriété BST doit être vraie pour chaque nœud parent suivant dans l'arborescence.
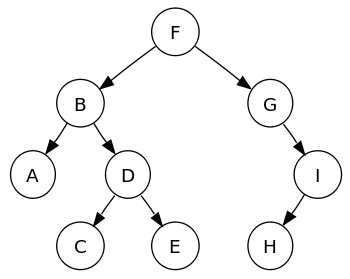
Les arbres de recherche binaires offrent une insertion et une recherche rapides. Les opérations d'insertion, de suppression et de recherche ont une complexité temporelle dans le pire des cas de O(n), qui est similaire à une liste chaînée.
Avantages des arbres binaires
Les arbres binaires offrent de nombreux avantages, c'est pourquoi ils restent une structure de données très utile. Ils peuvent être utilisés pour montrer les relations structurelles et les hiérarchies dans un ensemble de données. Plus important encore, les arbres binaires permettent une recherche, une suppression et une insertion efficaces.
Il est également très facile d'implémenter et de maintenir un arbre binaire. Un arbre binaire offre aux programmeurs les avantages d'un tableau ordonné et d'une liste chaînée; la recherche dans un arbre binaire est aussi rapide que dans un tableau trié et les opérations d'insertion ou de suppression sont aussi efficaces que dans les listes chaînées.
Les arbres binaires sont des structures de données importantes
Les arbres binaires sont une structure de données très importante et il est crucial que les programmeurs soient à l'aise de les appliquer dans leurs programmes. Souvent, les enquêteurs posent des problèmes d'arbre binaire simples tels que les traversées, la profondeur maximale, la mise en miroir, etc.
Nous vous recommandons fortement de comprendre le concept d'arbre binaire et de vous familiariser avec les problèmes d'entretien typiques.
TreeViz: un moyen simple de visualiser les structures de données
Lire la suite
- Programmation
- L'analyse des données
- Programmation

Fahad est écrivain à MakeUseOf et se spécialise actuellement en informatique. En tant que rédacteur technique passionné, il s'assure de rester à jour avec les dernières technologies. Il se retrouve particulièrement intéressé par le football et la technologie.
Abonnez-vous à notre newsletter
Rejoignez notre newsletter pour des conseils techniques, des critiques, des ebooks gratuits et des offres exclusives !
Cliquez ici pour vous abonner