7 algorithmes que tout programmeur devrait connaître

En tant qu'étudiant en programmation, vous avez probablement appris de nombreux algorithmes différents au cours de votre carrière. Devenir compétent dans différents algorithmes est absolument essentiel pour tout programmeur.

Avec autant d'algorithmes, il peut être difficile de garder une trace de ce qui est essentiel. Si vous vous préparez pour un entretien ou si vous perfectionnez simplement vos compétences, cette liste vous facilitera la tâche. Continuez à lire pendant que nous énumérons les algorithmes les plus essentiels pour les programmeurs.

1. Algorithme de Dijkstra

Edsger Dijkstra était l'un des informaticiens les plus influents de son temps et il a contribué à de nombreux domaines différents de l'informatique, y compris les systèmes d'exploitation, la construction de compilateurs et bien d'autres Suite. L'une des contributions les plus notables de Dijkstra est l'ingéniosité de son algorithme du chemin le plus court pour les graphiques, également connu sous le nom d'algorithme du chemin le plus court de Dijkstra.

L'algorithme de Dijkstra trouve le chemin le plus court dans un graphe d'une source à tous les sommets du graphe. À chaque itération de l'algorithme, un sommet est ajouté avec la distance minimale de la source et un qui n'existe pas dans le chemin le plus court courant. C'est la propriété gloutonne utilisée par l'algorithme de Djikstra.

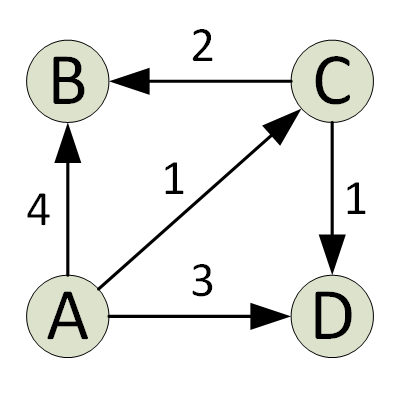
L'algorithme est généralement implémenté à l'aide d'un ensemble. L'algorithme de Dijkstra est très efficace lorsqu'il est implémenté avec un Min Heap; vous pouvez trouver le chemin le plus court en un temps O(V+ElogV) (V est le nombre de sommets et E est le nombre d'arêtes dans un graphe donné).

L'algorithme de Dijkstra a ses limites; cela ne fonctionne que sur les graphes orientés et non orientés avec des arêtes de poids positif. Pour les poids négatifs, l'algorithme de Bellman-Ford est généralement préférable.

Les questions d'entretien incluent généralement l'algorithme de Djikstra, nous vous recommandons donc vivement de comprendre ses détails complexes et ses applications.

2. Tri par fusion

Nous avons quelques algorithmes de tri sur cette liste, et le tri par fusion est l'un des algorithmes les plus importants. C'est un algorithme de tri efficace basé sur la technique de programmation Divide and Conquer. Dans le pire des cas, le tri par fusion peut trier « n » nombres en un temps O(nlogn). Par rapport aux techniques de tri primitives telles que Tri à bulles (cela prend du temps O(n^2)), le tri par fusion est extrêmement efficace.

En rapport: Introduction à l'algorithme de tri par fusion

Dans le tri par fusion, le tableau à trier est divisé à plusieurs reprises en sous-tableaux jusqu'à ce que chaque sous-tableau se compose d'un seul nombre. L'algorithme récursif fusionne ensuite à plusieurs reprises les sous-tableaux et trie le tableau.

3. Tri rapide

Quicksort est un autre algorithme de tri basé sur la technique de programmation Divide and Conquer. Dans cet algorithme, un élément est d'abord choisi comme pivot, et l'ensemble du tableau est ensuite partitionné autour de ce pivot.

Comme vous l'avez probablement deviné, un bon pivot est crucial pour un tri efficace. Le pivot peut être soit un élément aléatoire, l'élément média, le premier élément ou même le dernier élément.

Les implémentations de quicksort diffèrent souvent dans la façon dont elles choisissent un pivot. Dans le cas moyen, quicksort trie un grand tableau avec un bon pivot en un temps O(nlogn).

Le pseudocode général de quicksort partitionne à plusieurs reprises le tableau sur le pivot et le positionne dans la position correcte du sous-tableau. Il place également les éléments plus petits que le pivot à sa gauche et les éléments plus grands que le pivot à sa droite.

4. Recherche en profondeur d'abord

Depth First Search (DFS) est l'un des premiers algorithmes de graphes enseignés aux étudiants. DFS est un algorithme efficace utilisé pour parcourir ou rechercher un graphique. Il peut également être modifié pour être utilisé dans la traversée d'arbres.

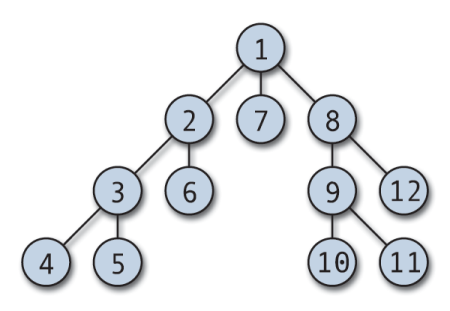
La traversée DFS peut commencer à partir de n'importe quel nœud arbitraire et plonge dans chaque sommet adjacent. L'algorithme revient en arrière lorsqu'il n'y a pas de sommet non visité ou qu'il y a une impasse. DFS est généralement implémenté avec une pile et un tableau booléen pour garder une trace des nœuds visités. DFS est simple à mettre en œuvre et exceptionnellement efficace; cela fonctionne (V+E), où V est le nombre de sommets et E est le nombre d'arêtes.

Les applications typiques de la traversée DFS incluent le tri topologique, la détection de cycles dans un graphe, la recherche de chemin et la recherche de composants fortement connectés.

5. Recherche en largeur d'abord

La recherche en largeur d'abord (BFS) est également connue sous le nom de parcours d'ordre de niveau pour les arbres. BFS fonctionne en O(V+E) comme un algorithme DFS. Cependant, BFS utilise une file d'attente au lieu de la pile. DFS plonge dans le graphique, tandis que BFS parcourt le graphique dans le sens de la largeur.

L'algorithme BFS utilise une file d'attente pour suivre les sommets. Les sommets adjacents non visités sont visités, marqués et mis en file d'attente. Si le sommet n'a pas de sommet adjacent, un sommet est supprimé de la file d'attente et exploré.

BFS est couramment utilisé dans les réseaux peer-to-peer, le chemin le plus court d'un graphe non pondéré, et pour trouver l'arbre couvrant minimum.

6. Recherche binaire

Recherche binaire est un algorithme simple pour trouver l'élément requis dans un tableau trié. Cela fonctionne en divisant à plusieurs reprises le tableau en deux. Si l'élément requis est plus petit que l'élément le plus au milieu, le côté gauche de l'élément du milieu est traité davantage; sinon, le côté droit est réduit de moitié et recherché à nouveau. Le processus est répété jusqu'à ce que l'élément requis soit trouvé.

La complexité temporelle dans le pire des cas de la recherche binaire est O(logn), ce qui la rend très efficace pour rechercher des tableaux linéaires.

7. Algorithmes Spanning Tree minimum

Un arbre couvrant minimum (MST) d'un graphe a le coût minimum parmi tous les arbres couvrants possibles. Le coût d'un arbre couvrant dépend du poids de ses bords. Il est important de noter qu'il peut y avoir plus d'un arbre couvrant minimum. Il existe deux principaux algorithmes MST, à savoir Kruskal et Prim.

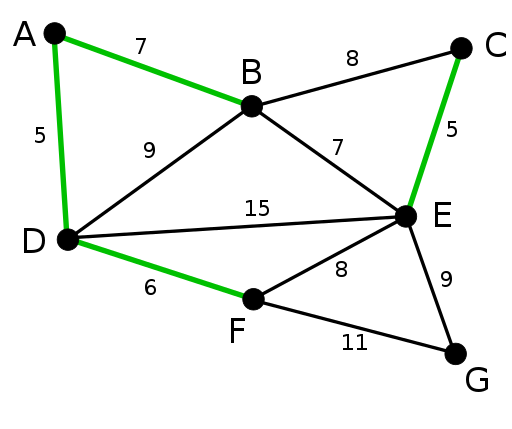
L'algorithme de Kruskal crée le MST en ajoutant l'avantage avec un coût minimum à un ensemble croissant. L'algorithme trie d'abord les arêtes par leur poids, puis ajoute des arêtes au MST en partant du minimum.

Il est important de noter que l'algorithme n'ajoute pas d'arêtes qui forment un cycle. L'algorithme de Kruskal est préféré pour les graphes clairsemés.

L'algorithme de Prim utilise également une propriété gloutonne et est idéal pour les graphiques denses. L'idée centrale du MST de Prim est d'avoir deux ensembles distincts de sommets; un ensemble contient le MST croissant, tandis que l'autre contient des sommets inutilisés. À chaque itération, le bord de poids minimum qui reliera les deux ensembles est sélectionné.

Les algorithmes d'arbre couvrant minimum sont essentiels pour l'analyse de cluster, la taxonomie et les réseaux de diffusion.

Un programmeur efficace maîtrise les algorithmes

Les programmeurs apprennent et développent constamment leurs compétences, et il y a quelques éléments essentiels que tout le monde doit maîtriser. Un programmeur qualifié connaît les différents algorithmes, les avantages et les inconvénients de chacun, et quel algorithme serait le plus approprié pour un scénario donné.

Une introduction à l'algorithme de tri Shell

Bien que le tri par shell ne soit pas la méthode la plus efficace, les débutants ont beaucoup à gagner à la pratiquer.

Lire la suite

A propos de l'auteur